Bidirectional Path Tracing 4 - A tweak of the filter

In Veach97 10.3.1 each pixel value \(I_{j}\) in the image is defined as a weighted average

$$I_{j} = \int\int_{D}h_{j}(u, v)I(u, v)dudv$$

where \(D\) is the image region (in world space, not pixel space), and \(h_{j}\) is the filter function (for example, a 2x2 box filter) for pixel j. When the filter function satisfies the criteria that \(\int\int_{D}h_{j}(u, v)dudv=1\), we filtered the measurement equation integration result \(I\) across lens and film area to one particular pixel \(I_{j}\) . This is a bit counter intuitive for me at the beginning: The measurement equation measure up a value related to the whole lens and film, and pixel value (what image rendering is actually looking for) is a post process product from the measurement value (by multiply importance \(W_{e}(x, \omega)\) and filter \(h_{j}(u, v)\) ) .

Since measurement equation contains integration across the whole film ( the \(D\) region), the samples we cast should be thrown across the whole film (For example, a 640x480 image with 4 samples per pixel, we throw out 640x480x4 samples to get the image value for pixel (123, 456). It doesn't sound make sense at first, but thinking further, all the other samples that pixel (123, 456) doesn't take get accumulated to other pixels, so we are not doing wasted work after all) The estimator for this equation would then be:

$$E(I_{j}) = 1/N \sum_{i=1}^{N}h_{j}(u_{i}, v_{i})I(u_{i}, v_{i}) / pdf_{A_{film}}(u_{i}, v_{i}) = D/N \sum_{i=1}^{N}h_{j}(u_{i}, v_{i})I(u_{i}, v_{i}) $$

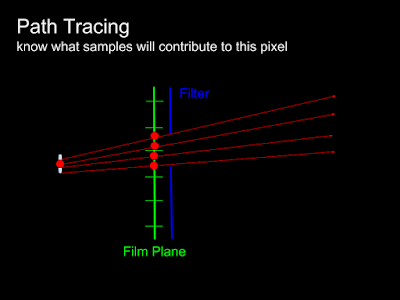
In the path tracing world that shooting ray from camera, we usually know which samples will contribute to a certain pixel (continue the 2x2 box filter example, the final (123, 456) pixel value would only be affect by the ray shooting across range (122, 455)->(124, 457) )  In fact, the filter equation usually used for path tracing looks like:

$$E(I_{j}) = \frac{\sum_{i=1}^{N}h_{j}(u_{i}, v_{i})I(u_{i}, v_{i})}{\sum_{i=1}^{N}h_{j}(u_{i}, v_{i})}$$

The coding logic is roughly like: for each sample we got a radiance value, we add value \(h_{j}(u_{i}, v_{i})I(u_{i}, v_{i})\) across region this sample centered kernel can cover to the covered pixels, and add \(h_{j}(u_{i}, v_{i})\) to a separate weight value associated to that pixel. At the end, we normalize each pixel with their associated weight. This works for camera based tracing method since, again, we know which samples would contribute to which pixel. This doesn't work for light tracing method since, for each ray shoot out from light, we don't know which pixel it will slam on film after bouncing around the scene.

As a result, Veach97 10.3.4.3 propose that using equation \(E(I_{j}) = \frac{\sum_{i=1}^{N}h_{j}(u_{i}, v_{i})I(u_{i}, v_{i})}{ \sum_{i=1}^{N}h_{j}(u_{i}, v_{i})}\) for path tracing method, and use \(E(I_{j})= D/N \sum_{i=1}^{N}h_{j}(u_{i}, v_{i})I(u_{i}, v_{i})\) for light tracing method. That is, for light tracing method, we throw out total N samples, whenever a sample hit the film and lens, we added the sample contribution \(h_{j}(u_{i}, v_{i})I(u_{i}, v_{i})\) to nearby affected pixels. At the end, we multiply the whole image film by factor \(D/N\) where \(D\) is the film area in world space.

My previous filtering implementation use the path tracing method above, and there is one missing puzzle that need to be filled to get the light tracing method work: \(\int\int_{D}h_{j}(u, v)dudv=1\) . The filter was not normalized to film world area space, for example, again the 2x2 box filter, \(h_{j}(u_{i}, v_{i}) = 1 \) if \((u_{i}, v_{i})\) is in the 2x2 kernel range else 0, the integration result for this filter would be 2x2 = 4 pixel area. To normalize this box filter, \(h_{j}(u_{i}, v_{i}) \) need to be divide by 4 pixel area so the final kernel integration become 1. I added a virtual method getNormalizedTerm for all filters to query kernel integration result in pixel space, and during the adding sample to final image space, I add in one more divide by pixel area step to normalize pixel space integration to world space. The reason I didn't put thing together is that I don't want the filter functionality depends on film size (which should able to change its size without worrying about what filter it's paired to) So here we go, the getNormalizedTerm :


And the related film constructor/addSample changes:

One thing that I feel a bit awkward is that it's actually not a easy thing to integrate Gaussian filter in finite range (surprise! consider how beautiful it converge when integrate to infinity) that turns out I use a clumsy numerical approximation to get an approximated integration result. It's not really beautiful, but it serves the purpose ;)

In the next post I would like to write down the thoughts while looking in Veach97 10.2 : the ways to form a path, and its contribution to the final measurement (which is the \alpha weight I briefly mentioned in previous post ) It will be the ground work to start writing light tracing, and push it further to bidirectional path tracing.